Loin d'être une science abstraite réservée aux spécialistes, la sensitométrie est un pilier de la photographie comme le sont la photométrie et l'optique. Aussi, il nous semble utile d'en souligner les principes fondamentaux, rudiments indispensables pour mieux comprendre et dominer le mécanisme du processus photographique.
Définition de la sensitométrie
Etymologiquement, « sensitométrie » signifie mesure de la sensibilité mais en réalité, le sens du terme est étendu à tout ce qui a trait aux propriétés et caractéristiques des surfaces sensibles. Ce sont les savants Hurter et Driffield qui ont établi à la fin du 19me siècle, les principes de la sensitométrie qui depuis, sont appliqués dans le monde entier. Ce n'est donc pas une science récente. Certes, avec le progrès de la technologie dans l'industrie des surfaces sensibles et du matériel photographique, les méthodes de mesure se sont affinées mais les règles fondamentales demeurent.
 |
 |
|
| Ferdinand Hurter (1844-1898) | Vero Charles Driffield (1848-1915) |
Grâce aux travaux (résultats publiés en 1890) de Ferdinand Hurter et Vero Charles Driffield, fondateurs de la sensitométrie, on peut parler d’une mathématisation de la photographie. Ces pionniers, en étudiant les réponses de surfaces photographiques exposées à différentes « quantités de lumière », ont pu notamment, pour la première fois, tracer la courbe sensitométrique des surfaces sensibles explorées et ainsi représenter mathématiquement cette relation (densités en fonction du logarithme des luminations incidentes). Une courbe de noircissement photographique appelée aussi courbe H&D en l’honneur de ces deux savants qui ont fait passer la photographie du domaine de l’empirisme à celui de la science ! |
Lumination / noircissement
La sensitométrie n'est absolument rien d'autre que l'analyse de ce rapport de cause à effet. A la répartition des différentes luminations sur la couche sensible, correspond après développement, celle des différentes valeurs de noircissement du négatif. Plus la lumination est importante, plus le noircissement est dense, c'est-à-dire plus il y a de cristaux d'halogénures d'argent de l'émulsion photographique réduits en argent métallique de couleur noire. Aux hautes lumières de l'image du sujet, correspond donc un noircissement intense et inversement pour les ombres.
Opacité
Si nous observons le négatif par transparence, sa perméabilité à la lumière pour une plage donnée est évidemment fonction du degré de noircissement de cette plage. Le degré de noircissement ou « non transparence » appelé plus exactement opacité (Op) se définit par le rapport du flux lumineux incident sur le flux transmis.
Considérons au hasard une plage d'un négatif soumis à un flux lumineux incident de 100 (en valeurs relatives). Ce flux est en partie absorbé par les minuscules particules d'argent métallique. Si le flux transmis a une valeur de 2, l'opacité du dépôt d'argent de la plage en question est donc égal à 50. Nous remarquons en passant que l'opacité varie dans le même sens que le noircissement.
Densité
En général, les opacités des négatifs photographiques s'échelonnent de 1 à 1000 mais quelquefois dépassent ce dernier nombre. Aussi, à la place de ces valeurs arithmétiques souvent très élevées et se prêtant mal à une représentation graphique, préfère-t-on utiliser – comme à la prise de vue en ce qui concerne les valeurs de luminance et de lumination – les logarithmes décimaux correspondants.
Le logarithme décimal de l'opacité est appelé densité optique ou tout simplement densité (D). Nous avons ainsi la relation : D = log Op. En pratique, pour représenter les différents degrés de noircissement d'un négatif, ce sont donc les valeurs de densité qui sont utilisées plutôt que celles d'opacité. Le tableau ci-dessous donne, pour quelques valeurs d'opacité, la correspondance en densité :
Opacité |
Densité |
1,00 1,26 1,58 1,99 2,51 3,16 3,98 5,01 6,31 7,94 10,00 100,00 1000,00 10000,00 |
0,00 0,10 0,20 0,30 0,40 0,50 0,60 0,70 0,80 0,90 1,00 2,00 3,00 4,00 |
Utilisation de graphiques à coordonnées logarithmiques
En sensitométrie, on représente toujours la relation lumination / noircissement sur des graphiques à coordonnées logarithmiques, l'échelle étant la même pour les deux axes (figure 1). En abscisse, on porte les valeurs logarithmiques des luminations : log H. Attention, beaucoup d'auteurs utilisent l'expression log E à la place de log H mais à tort car E est le symbole de l'éclairement et non celui de la lumination (Système International d'unités). En ordonnée, sont portées les densités (D) qui sont, nous l'avons dit, des valeurs logarithmiques.
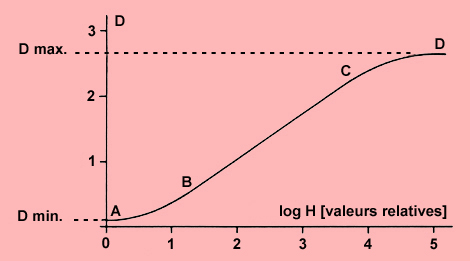
Figure 1 : Courbe caractéristique d'une émulsion négative. On distingue habituellement le pied (A-B), la partie centrale (B-C) et l'épaule (C-D). |
Tracé et description de la courbe caractéristique
Pour étudier les caractéristiques et les propriétés d'une émulsion photographique, le fabricant soumet celle-ci à une série de luminations croissantes au moyen d'un instrument appelé sensitomètre. L'échantillon exposé ou sensitogramme est ensuite traité et les densités obtenues, mesurées à l'aide d'un densitomètre. Sur un graphique, comme décrit ci-dessus, sont portées les différentes valeurs de densité correspondant aux valeurs respectives de lumination. En reliant les différents points, on obtient une courbe de noircissement qui est caractéristique de l'émulsion étudiée. Une courbe appelée aussi courbe H&D en l’honneur des deux savants (Hurter et Driffield) qui ont fait passer la photographie du domaine de l’empirisme à celui de la science !
La figure 1 représente la courbe caractéristique d'une émulsion. Nous remarquons que la densité n'augmente proportionnellement à la valeur log H que dans la partie rectiligne de la courbe (B-C). Autrement dit, dans cette zone centrale correspondant aux luminations moyennes, le rapport entre densité et log H est constant. Inversement, dans les deux zones extrêmes de la courbe, le rapport entre densité et log H n'est plus constant. Ces zones appelées communément pied (A-B) et épaule (C-D) admettent respectivement les faibles et les fortes luminations.
Plus explicitement, la différenciation (ou séparation) des tons est optimum là où la pente atteint son niveau le plus élevé c'est-à-dire dans la portion linéaire de la courbe. Par contre, dans les deux portions curvilignes, au fur et à mesure de la réduction de la pente, on assiste à une « compression » des tons ; la différenciation des valeurs du négatif s'adoucit progressivement jusqu'à une disparition totale des détails lorsque la pente devient nulle. L'opérateur veillera donc – c'est un des premiers enseignements d'une courbe caractéristique – à ne pas enregistrer de luminations de l'image du sujet, notamment celles des ombres et des hautes lumières, dans les points du pied ou de l'épaule de la courbe où la pente n'est pas suffisante pour engendrer une séparation de tons acceptable sur le négatif. Nous aurons souvent l'occasion dans ces pages techniques de parler du respect et de la mise en pratique de cette règle élémentaire.
Notons enfin que lorsque la lumination est nulle, il existe toujours une certaine densité (densité minimum ou D min.) due au support du film qui n'est pas absolument transparent et au voile d'émulsion, noircissement parasite lié à la nature même de l'émulsion (D min. = D support + voile). A l'opposé, l'épaule de la courbe atteint une densité maximum (D max.).
La pente de la courbe caractéristique
Nous savons que les valeurs du sujet sont parfaitement transcrites lorsque les densités sont proportionnelles au logarithme des luminations. Or, cette condition ne se réalise que dans la zone centrale de la courbe caractéristique (B-C, figure 1), partie rectiligne dont la pente est un critère important. Ce dernier indique le rapport existant entre le contraste du négatif et celui de l'image du sujet.
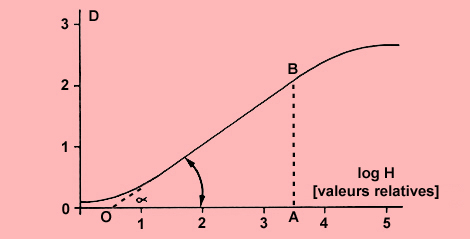
Figure 2 : Détermination de la pente de la partie rectiligne de la courbe caractéristique. |
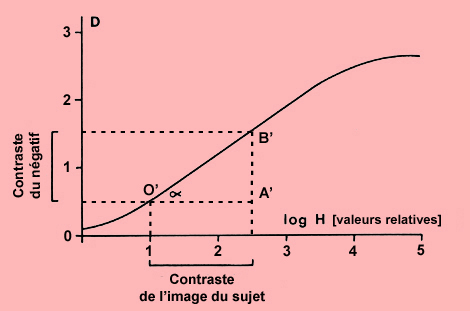
Figure 3 : On peut aussi définir la tangente de l'angle alpha en construisant un triangle rectangle semblable O'A'B'.
|
Un moyen de déterminer la pente consiste à prolonger la partie rectiligne jusqu'à l'abscisse (figure 2). La tangente de l'angle (angle alpha) formé par cette droite et l'axe horizontal définit la pente. De même (figure 3 où est dessinée la même courbe), on peut définir la tangente de l'angle alpha en construisant un triangle rectangle semblable O'A'B' de façon à faire correspondre A'B' (intervalle entre densités extrêmes = contraste du négatif) avec O'A' (intervalle entre luminations extrêmes = contraste de l'image du sujet), l'unité de mesure étant la même pour A'B' et O'A'.
Plus la pente est élevée, plus la valeur tg alpha est grande. Lorsque la pente est de 45°, tg alpha = 1, valeur signifiant qu'un accroissement donné de la lumination (log H) entraîne une augmentation équivalente de la densité. La relation tg alpha = contraste du négatif / contraste de l'image du sujet permet de déterminer le contraste du négatif qui est donc égal au contraste de l'image du sujet x tg alpha.
